从零实现一个数据血缘拓扑图

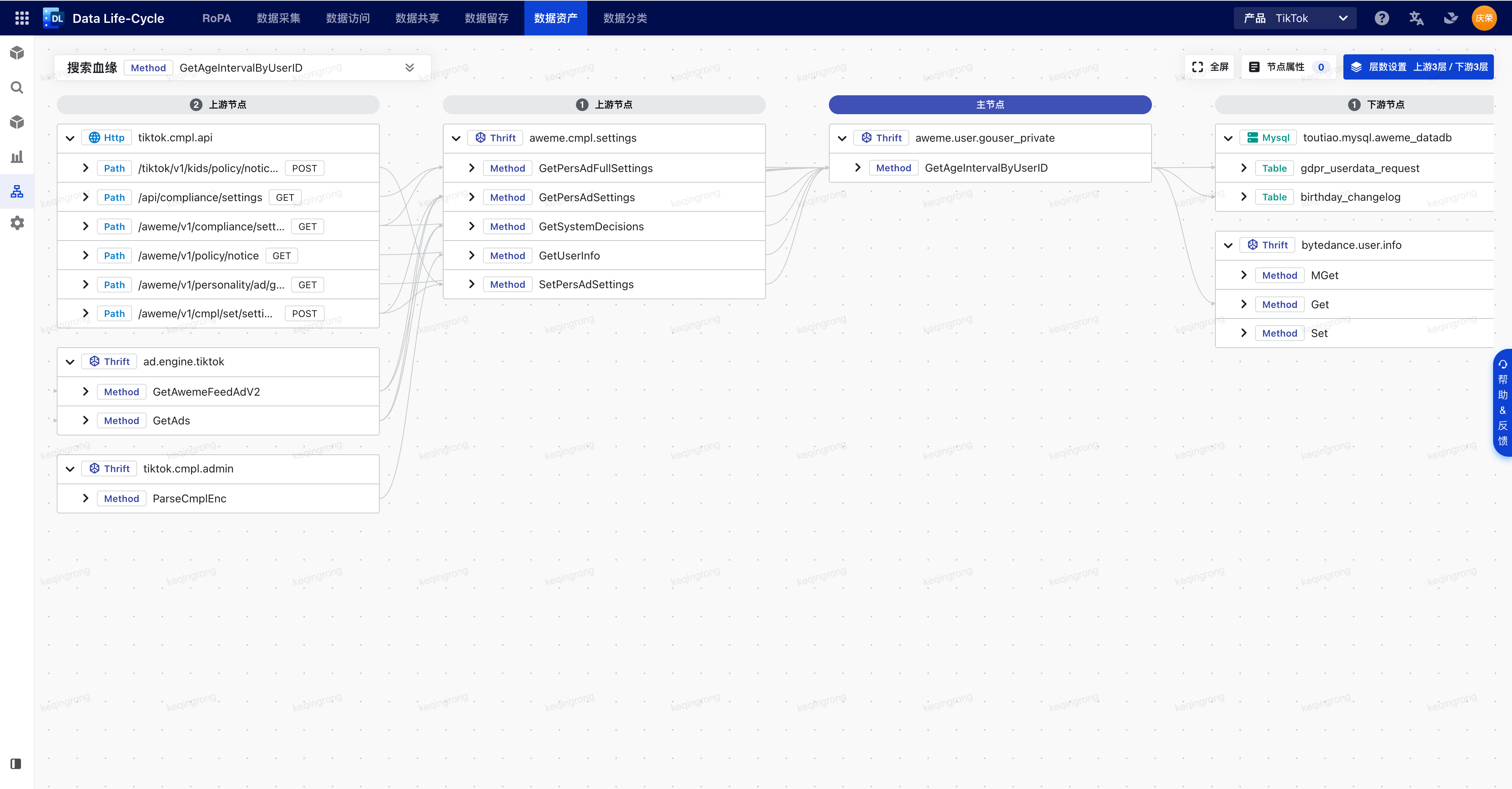
节选自笔者在团队内做的一次技术分享，介绍了2022年7月从零开发的第一版数据血缘拓扑图实现逻辑。特别说明，原文档为飞书文档，转成Markdown后，图例有所丢失。

背景
- 为什么选择自研拓扑图？
如何实现数据血缘拓扑图？
详细实现
实现效果

背景

为什么选择自研拓扑图？

主要有两点原因：

业界缺少我们需要的拓扑图方案

常规的有向图基于节点，数据血缘拓扑图基于Tree，我们所要构建的图不局限于Graph with Asset Field Node，而希望和资产平台对齐，实现Graph with Asset PSM Tree。

缺少现成的布局算法

目前缺少成熟的类似层次布局算法（Dagre）、d3-hierarchy、力导向图布局算法（Force-directed graph）这样的布局算法，需要自行实现布局，计算各点坐标位置。

如何实现数据血缘拓扑图？

自研拓扑图需要解决的核心问题：

如何计算布局，生成节点位置坐标？
如何绘制边？
如何绘制节点？

如何计算布局

在绘制边之前，首先要进行布局计算，获取边的起始点和目标点的位置坐标。

主要有两种思路：

使用特定布局算法计算位置坐标，如层次布局算法、力导向图布局算法
交给浏览器布局，渲染后获取位置坐标

前期调研的可选方案都是基于这两种思路实现：

Antv G6/X6、React Flow

使用 dagre 的层次布局算法，提前计算所有节点位置信息。

@tiktok-woody/react-dag

使用 dagre 的层次布局算法计算节点位置，同时在节点挂载后将节点的ID和DOM引用保存到Store中，使得外层可以通过ID操作节点DOM，进而调整节点位置。

Coral xGraph (DataLineageGraph)

节点的宽高固定，节点组的外间距固定，根据节点组的位置和节点的索引提前计算节点位置。滚动时基于节点组内滚动偏移量，重新计算节点位置。

本血缘拓扑图参考 Coral 的多列布局形式，因此无法使用 dagre 的层次布局算法，又因为需要支持自定义节点和做粗粒度节点展开，只能在节点渲染挂载后使用 getBoundingClientRect() 获取位置。滚动时可以综合原位置信息和滚动偏移量，或者重新调用 getBoundingClientRect() 获取最新位置。

如何同步布局

由于节点组内部支持垂直滚动，当用户滚动后需要同步最新的节点位置信息，重新绘制边。

上层被动接收下层节点在挂载后发布的宽高和位置数据（缺点：节点组滚动时，节点内部无法感知 scroll 事件）
上层主动获取下层节点的宽高和位置信息
- a. 自底向上：下层节点增加 DOM ID，上层使用 document.getElementById() 获取节点 DOM（缺点：违背 React 设计原则）
- b. 自底向上：下层节点增加 ref，借助 Context 传给上层，上层从 Context 中获取节点 DOM
- c. 自顶向下：上层为所有下层节点统一创建 ref，通过 Context 分发给下层节点，上层从 ref 集合中获取节点 DOM

本血缘拓扑图采用方案2-b，布局变化后由上层主动调用DOM API获取下层节点的宽高和位置信息。

使用什么方案绘制边

获取起始点和目标点的位置坐标后便可以绘制边。

基于Canvas
- API：lineTo()、quadraticCurveTo()、bezierCurveTo()
- 代表：Coral xGraph (DataLineageGraph)、Antv G6
- 优势：高性能
- 劣势：只能通过Canvas API修改样式；事件监听只能绑定在Canvas容器上，需要手动分发事件。
基于SVG
- SVG元素：<line>、<polyline>、<path>
- 代表：@tiktok-woody/react-dag、Antv X6、React Flow
- 优势：矢量，支持缩放；支持CSS和DOM事件
- 劣势：节点数量到达一定量级后性能较差

本血缘拓扑图采用SVG方案，和Canvas相比，它支持定义边的鼠标事件，可以通过CSS控制样式。

注意：2022年7月数据血缘图的数据量最多只有几百个节点，边的数量大约是点的2.5倍；2023年3月，已经远远超出该数据量。

使用什么方案绘制节点

血缘拓扑图的节点绘制较为简单，采用 Semi Tree 实现 PSM -> Method -> Field 树，通过 renderFullLabel 属性接管树节点的渲染。

详细实现

组件设计

拓扑图节点、连线绘制层级

暂时无法在飞书文档外展示此内容

从下往上依次是：

背景层：绘制网格背景
连线层：绘制底层灰色连线
节点层：绘制节点，有跨层级连线时，上层节点将遮盖住连线
高亮连线层：绘制顶层蓝色连线，有跨层级连线时，连线将浮在节点上层

拓扑图数据源

图的数据源只需要包含构建节点和边的最基本字段。

interface Node<T> {
  id: string;
  data: T;
}

interface Edge<T> {
  source: string;
  target: string;
  data: T;
}

示例：

const data = {
  nodes: [
    {
      id: 'node1'
    },
    {
      id: 'node2'
    },
  ],
  edges: [
    {
      source: 'node1',
      target: 'node2'
    }
  ],
};

拓扑图组件结构

暂时无法在飞书文档外展示此内容

拓扑图组件 Props

interface Position {
  x: number;
  y: number;
}

interface Rect {
  width: number;
  height: number;
}

interface NodeProps {
  /** 节点唯一ID */
  id: string;
  /** 节点名称，可以同时存在于 data 字段中 */
  label?: string;
  /** 节点原点位置（左上角） */
  position?: Position;
  /** 节点宽高尺寸 */
  rect?: Rect;
  /** 节点数据 */
  data?: Record<string, unknown>;
  /** 子节点 */
  children?: Node[];
  /** 自定义节点渲染 */
  renderNode: (node: NodeProps) => RectNode;
  /** 节点点击回调 */
  onNodeClick: (node: NodeProps) => void;
  /** 节点展开回调 */
  onNodeExpand: (node: NodeProps) => void;
  /** 节点菜单选择回调  */
  onNodeContextMenuSelect?: (id: string, type: ContextMenuType) => void;
}

interface EdgeProps {
  /** 边唯一ID，默认使用 'source_target' 拼接 */
  id?: string;
  /** 起始点ID */
  source: string;
  /** 目标点ID */
  target: string;
  /** 边样式 */
  style?: CSSProperties;
}

interface ColumnProps {
  /** 上游/下游/终点 */
  type: 'upstream' | 'downstream' | 'endpoint';
  /** 层数，0表示当前节点/终点 */
  depth: number;
  /** 节点数据源 */
  nodes: NodeProps[];
  /** 自定义节点渲染 */
  renderNode: (node: NodeProps) => ReactNode;
  /** 节点点击回调 */
  onNodeClick: (node: NodeProps) => void;
  /** 节点展开回调 */
  onNodeExpand: (node: NodeProps) => void;
  /** 节点菜单选择回调  */
  onNodeContextMenuSelect?: (id: string, type: ContextMenuType) => void;
}

interface LineageGraphProps {
  /** 节点数据源 */
  nodes: NodeProps[];
  /** 边数据源 */
  edges: EdgeProps[];
  /** 主节点ID */
  primaryNodeId?: string;
  /** 展示层级 */
  level?: number;
  /** 自定义节点渲染 */
  renderNode: (node: NodeProps) => RectNode;
  /** 自定义遍渲染 */
  renderEdge: (edge: EdgeProps) => RectNode;
  /** 节点点击回调 */
  onNodeClick: (node: NodeProps) => void;
  /** 节点展开回调 */
  onNodeExpand: (node: NodeProps) => void;
  /** 节点菜单选择回调  */
  onNodeContextMenuSelect?: (id: string, type: ContextMenuType) => void;
}

LineageGraph JSX 示例代码：

<LayoutProvider>
  <EdgeProvider>
    <EdgeLayer edges={edges} />
    <HighlightedEdgeLayer edges={highlightedEdges} />
    <NodeLayer nodes={aggregatedNodes} />
  </EdgeProvider>
<LayoutProvider/>

其中

LayoutProvider 用于提供节点布局信息，如坐标位置、宽高、DOM引用
EdgeProvider 用于提供边的绘制信息，如是否已经绘制

坐标系换算

HTML、SVG、Canvas 都以页面的左上角为 (0, 0) 坐标点（原点），坐标以像素为单位，x 轴正方向是向右，y 轴正方向是向下。

由于 HTML 中 Event 事件、getBoundingClientRect() 获取的坐标位置始终相对于页面原点，当页面发生滚动后，获取的坐标并不能反映节点、连线在 SVG 容器中的真实位置，因此布局计算的全部坐标都需要相对 SVG 容器左上角原点做一定偏移。

interface Rect {
  width: number;
  height: number;
  x: number;
  y: number;
}

export const translate = (position?: DOMRect, origin = { x: 0, y: 0 }): Rect | undefined => {
  if (!position) {
    return undefined;
  } else {
    return {
      width: position.width,
      height: position.height,
      x: position.x - origin.x,
      y: position.y - origin.y,
    };
  }
};

// 起点原始Rect
const rect1 = ...
// 终点原始Rect
const rect2 = ...

// 起点坐标
const p1 = useMemo(() => translate(rect1, origin), [rect1, origin]);
// 终点坐标
const p2 = useMemo(() => translate(rect2, origin), [rect2, origin]);

分层

层级计算方案

以下分层方案按“主节点模式”说明。“起止点模式”层级计算方式和主节点模式类似，起始点记为0层，终止点记为Infinity无穷大层，将起点作为主节点计算层级。

方案一：按边的关系累加计算

主节点记为0层，以下游层级计算为例，和主节点有直接边关系的点，记为下游1层，和下游1层有直接边关系记为下游2层，依此类推。如果某节点已经赋过层级，有新的边关系时不再重新计算。

方案二：按节点和主节点的最短路径计算

基于Dijkstra算法（不允许有环）。

方案三：按节点和主节点的“最长路径”计算

无高效算法，有环的情况下无最长路径。

分层案例

案例1：3个节点

边关系：A -> B，A -> C，B -> C，其中A为主节点。

方案	示意图
按最短路径计算，B、C是下游1层。	暂时无法在飞书文档外展示此内容
按最长路径计算，B是下游1层，C是下游2层。	暂时无法在飞书文档外展示此内容

案例2：4个节点

边关系：A -> B，B -> C，C -> D，A-> D，其中A为主节点。

方案	示意图
按最短路径计算，B、D是下游1层，C是下游2层。	暂时无法在飞书文档外展示此内容
按最长路径计算，B是下游1层，C是下游2层，D是下游3层。	暂时无法在飞书文档外展示此内容
按边关系累加计算，情况1同最短路径；情况2，B、C、D是下游1层。（避免了图中出现从右到左的反向箭头）	暂时无法在飞书文档外展示此内容

案例3：5个节点

边关系：A -> B，B -> C，C -> D，A -> E，E -> D，其中A为主节点。

方案	示意图
按最短路径计算，B、E是下游1层，C、D是下游2层。	暂时无法在飞书文档外展示此内容
按最长路径计算，B、E是下游1层，C是下游2层，D是下游3层。	暂时无法在飞书文档外展示此内容
按边关系累加计算，结果同最短路径。	暂时无法在飞书文档外展示此内容

代码实现

import { Node, Edge, GraphDataSource } from '../types';

interface DepthResult {
  depth2ids: Record<number, string[]>;
  id2depth: Record<string, number>;
}

/**
 * 主节点模式血缘图分层计算（按边关系累加计算）
 */
export const calcSingleGraphDepths = (graph: GraphDataSource, primaryId: string): DepthResult => {
  const id2depth: Record<string, number> = { [primaryId]: 0 };
  const depth2ids: Record<number, string[]> = {};
  const { nodes, edges } = graph;

  // 已经进行过分层，直接使用已有的depth
  const depthCalculated = nodes.find((node: Node) => typeof node.data?.depth === 'number');
  if (depthCalculated) {
    nodes.forEach((node: Node) => {
      if (typeof node.data?.depth === 'number') {
        const depth = node.data.depth;
        if (depth2ids[depth]) {
          depth2ids[depth].push(node.id);
        } else {
          depth2ids[depth] = [node.id];
        }
      }
    });
  } else {
    // 保证主节点Tree上所有节点depth都为0
    let primaryIdRootId = primaryId;
    const primaryNode = nodes.find((node: Node) => node.id === primaryId);
    if (primaryNode?.data) {
      primaryIdRootId = primaryNode.data.rootId;
    }
    const primaryNodeList = nodes.filter((node: Node) => node?.data?.rootId === primaryIdRootId);
    primaryNodeList.forEach((node: Node) => {
      id2depth[node.id] = 0;
    });

    // 计算当前节点直接上下游的相对层级
    const calcRelativeDepth = (id: string, depth = 0) => {
      if (depth2ids[depth]) {
        depth2ids[depth].push(id);
      } else {
        depth2ids[depth] = [id];
      }
      
      // 查找直接上下游
      const keys = Object.keys(id2depth);
      const associatedEdges = edges.filter(({ source, target }: Edge) => {
        return (source === id && !keys.includes(target)) || (target === id && !keys.includes(source));
      });

      const associatedNodeDepthMap: Record<string, number> = {};

      // 计算当前节点上下游层级
      associatedEdges.forEach(({ source, target }: Edge) => {
        const associatedNodeId = source === id ? target : source;
        let associatedNodeDepth = source === id ? depth + 1 : depth - 1;
        if (associatedNodeDepth === 0) {
          // 当下级或上级同主节点相同的层级，将其往上或者下层放
          associatedNodeDepth = source === id ? depth - 1 : depth + 1;
        }
        if (!id2depth[associatedNodeId]) {
          id2depth[associatedNodeId] = associatedNodeDepth;
        }
        // 保存当前节点上下游
        associatedNodeDepthMap[associatedNodeId] = associatedNodeDepth;
      });
      
      // 计算上下游的上下游
      Object.entries(associatedNodeDepthMap).forEach(([nodeId, nodeDepth]) => {
        calcRelativeDepth(nodeId, nodeDepth);
      });
    };

    calcRelativeDepth(primaryId);
  }

  return {
    depth2ids,
    id2depth,
  };
};

粒度聚合和展开

PSM 粒度展开

初始为PSM粒度：

暂时无法在飞书文档外展示此内容

PSM展开后：边关系保持PSM粒度，不额外请求Method、Field粒度边关系数据

暂时无法在飞书文档外展示此内容

Field 粒度聚合

初始为Field粒度：

暂时无法在飞书文档外展示此内容

Field聚合成PSM后：节点按PSM-Method-Field形式渲染，边关系保持Field粒度

暂时无法在飞书文档外展示此内容

数据聚合实现

示例数据，处理前：

// `path_info` 为父级节点列表
const nodes = [
  { id: 'aaa', path_info: [{ id: 'a' }, { id: 'aa' }] },
  { id: 'baa', path_info: [{ id: 'b' }, { id: 'ba' }] },
  { id: 'bab', path_info: [{ id: 'b' }, { id: 'ba' }] },
  { id: 'bac', path_info: [{ id: 'b' }, { id: 'ba' }] },
  { id: 'bba', path_info: [{ id: 'b' }, { id: 'bb' }] },
  { id: 'caa', path_info: [{ id: 'c' }, { id: 'ca' }] }
];

const edges = [
  { source: 'aaa', target: 'baa' },
  { source: 'aaa', target: 'bab' },
  { source: 'aaa', target: 'bac' },
  { source: 'aaa', target: 'bba' },
  { source: 'aaa', target: 'caa' }
];

示例数据，处理后：

const aggregatedNodes = [
  {
    id: 'a',
    children: [{ id: 'aa', children: [{ id: 'aaa' }] }]
  },
  {
    id: 'b',
    children: [
      { id: 'ba', children: [{ id: 'baa' }, { id: 'bab' }, { id: 'bac' }] },
      { id: 'bb', children: [{ id: 'bba' }] }
    ]
  },
  { 
    id: 'c',
    children: [{ id: 'ca', children: [{ id: 'caa' }] }]
  }
];

const aggregatedEdges = [
  { source: 'a', target: 'b' },
  { source: 'a', target: 'c' }
];

代码实现：

import { NodeVariantData, NodeVariant, EdgeVariant } from './types';

interface Options {
  nodes?: NodeVariant<NodeVariantData>[];
  edges?: EdgeVariant[];
}

interface Result {
  nodes: NodeVariant[];
  edges: EdgeVariant[];
}

/**
 * 对血缘图数据源进行聚合，将扁平数据处理成psm->method->field树形数据
 */
export const aggregate = ({ nodes = [], edges = [] }: Options): Result => {
  const nodeMap: Record<string, NodeVariant> = {};
  const aggregatedNodes: NodeVariant[] = [];
  const aggregatedEdges: EdgeVariant[] = [];

  // 聚合 node
  nodes.forEach((node) => {
    if (!nodeMap[node.id]) {
      nodeMap[node.id] = { ...node };
    }

    // 如果有祖先节点列表，则从左往右处理，第一个节点push到aggregatedNodes中，剩余节点作为前一个节点的子节点；
    // 如果没有祖先节点列表，则将当前节点push到aggregatedNodes中。
    const ancestors = node?.data?.ancestors ?? [];

    [...ancestors, node].reduce<NodeVariant | null>((previous, current) => {
      if (!nodeMap[current.id]) {
        nodeMap[current.id] = {
          id: current.id,
          label: current.label,
        };
      }
      const currentNode = nodeMap[current.id];

      if (!previous) {
        if (!aggregatedNodes.find((item) => item.id === current.id)) {
          aggregatedNodes.push(currentNode);
        }
      } else {
        (currentNode.data as NodeVariantData).parentId = previous.id;
        const previousNode = nodeMap[previous.id];
        if (!Array.isArray(previousNode.children)) {
          previousNode.children = [];
        }
        if (!nodeMap[previous.id].children?.find((child) => child.id === current.id)) {
          previousNode.children?.push(currentNode);
        }
      }
      return current;
    }, null);
  });

  const appendRootId = (list: NodeVariant[], rootId?: string) => {
    list.forEach((item) => {
      if (rootId) {
        (item.data as NodeVariantData).rootId = rootId;
      } else {
        (item.data as NodeVariantData).rootId = item.id;
      }
      if (Array.isArray(item.children)) {
        appendRootId(item.children, item.data?.rootId);
      }
    });
  };

  // 增加 rootId，方便聚合 edge
  appendRootId(aggregatedNodes);

  // 聚合 edge
  edges.forEach((edge) => {
    const source = nodeMap[edge.source]?.data?.rootId;
    const target = nodeMap[edge.target]?.data?.rootId;
    if (source && target) {
      const id = `${source}_${target}`;
      if (!aggregatedEdges.find((item) => item.id === id)) {
        aggregatedEdges.push({
          id,
          source,
          target,
        });
      }
    }
  });

  return {
    nodes: aggregatedNodes,
    edges: aggregatedEdges,
  };
};

边的绘制

SVG 路径绘制

如果想了解更多，可以参考如下链接：

MDN path 教程 https://developer.mozilla.org/en-US/docs/Web/SVG/Tutorial/Paths

SvgPathEditor https://yqnn.github.io/svg-path-editor/

三次贝塞尔曲线动画 https://cubic-bezier.com/

SVG元素	说明	示例代码
`<line>`	用于创建一条连接两个点的直线。主要属性： - x1 定义起点x坐标 - x2 定义起点y坐标 - y1 定义终点x坐标 - y2 定义终点y坐标	`<svg viewBox="0 0 100 100" xmlns="http://www.w3.org/2000/svg"> <line x1="0" y1="80" x2="100" y2="20" stroke="black" /> </svg>`
`<polyline>`	用于创建多段直线。主要属性： - points 定义需要绘制的点的x、y坐标列表	`<svg viewBox="0 0 200 100" xmlns="http://www.w3.org/2000/svg"> <polyline points="100,100 150,25 150,75 200,0" fill="none" stroke="black" /> </svg>`
`<path>`	用于创建复杂的SVG形状。主要属性： - d 定义绘制的路径命令列表	`<svg viewBox="0 0 100 100" xmlns="http://www.w3.org/2000/svg"> <path fill="none" stroke="red" d="M 10,30 A 20,20 0,0,1 50,30 A 20,20 0,0,1 90,30 Q 90,60 50,90 Q 10,60 10,30 z" /> </svg>`

SVG 定义了六种路径命令类型，一共 20 条命令：

移动到（Move To）：M、m
画线到（Line To）：L、l、H、h、V、v
三次贝塞尔曲线（Cubic Bézier Curve）：C、c、S、s
二次贝塞尔曲线（Quadratic Bézier Curve）：Q、q、T、t
弧线/椭圆曲线（Arc）：A、a
封闭路径：Z、z

SVG 代码

<!-- 普通边 -->
<svg class="edge-layer">
  <defs>
    <!-- 箭头 -->
    <marker
      id="arrow"
      viewBox="0 -5 10 10"
      refX="9"
      refY="0"
      markerWidth="5"
      markerHeight="5"
      orient="auto"
    >
      <path d="M 0,-5 L 10,0 L 0,5" stroke="#C6CACD" fill="#C6CACD" />
    </marker>
  </defs>
  <!-- 一条终点为箭头的边 -->
  <path d="M 920,105 C 960,105 960,105 1000,105" class="path-curve" marker-end="url(#arrow)"></path>
</svg>

<!-- 高亮边 -->
<svg class="edge-layer">
  <defs>
    <!-- 高亮箭头 -->
    <marker
      id="arrow-highlighted"
      viewBox="0 -5 10 10"
      refX="9"
      refY="0"
      markerWidth="5"
      markerHeight="5"
      orient="auto"
    >
      <path d="M 0,-5 L 10,0 L 0,5" stroke="#0077FA" fill="#0077FA" />
    </marker>
  </defs>
  <!-- 一条终点为高亮箭头的边 -->
  <path d="M 920,106 C 960,106 960,105 1000,105" class="path-curve path-active" marker-end="url(#arrow-highlighted)"></path>
</svg>

CSS 代码

.edge-layer {
  width: 100%;
  height: 100%;
}

.edge-layer-highlighted {
  pointer-events: none;
}

.path-curve {
  fill: none;
  stroke: #c6cacd;
  stroke-width: 1;
}

.path-active {
  stroke: #0e42d2;
  stroke-dasharray: 4;
  stroke-width: 1;
}

SVG 动画

采用 CSS 动画实现，通过周期性修改 stroke dash array 的偏移量。

@keyframes dash {
  from {
    stroke-dashoffset: 60;
  }
  to {
    stroke-dashoffset: 10;
  }
}

.path-curve {
  fill: none;
  stroke: #c6cacd;
  stroke-width: 1;
}

.path-active {
  stroke: #0e42d2;
  stroke-dasharray: 4;
  stroke-width: 1;
  animation: dash 4s linear infinite normal;
}

边的绘制场景

边关系	场景：A、B同列	场景：A、B相邻列	场景：A、B跨列
A->A	暂时无法在飞书文档外展示此内容暂时无法在飞书文档外展示此内容	无	无
A->B，A、B同层	无	方案1：左入右出：暂时无法在飞书文档外展示此内容	方案1：左入右出（不避让）：暂时无法在飞书文档外展示此内容方案1：左入右出（避让）：暂时无法在飞书文档外展示此内容
A->B，A、B不同层	方案1：左入右出：暂时无法在飞书文档外展示此内容方案2：从上往下时右入右出，从下往上时左入左出：暂时无法在飞书文档外展示此内容	方案1：左入右出：暂时无法在飞书文档外展示此内容	方案1：左入右出（不避让）：暂时无法在飞书文档外展示此内容方案2：左入右出（避让）：暂时无法在飞书文档外展示此内容
A->B, B->A	方案1：左入右出：暂时无法在飞书文档外展示此内容方案2：从上往下时右入右出，从下往上时左入左出：暂时无法在飞书文档外展示此内容	方案1：左入右出：暂时无法在飞书文档外展示此内容方案2：从上往下时右入右出，从下往上时左入左出：暂时无法在飞书文档外展示此内容方案3：出入共用一条边暂时无法在飞书文档外展示此内容	方案1：左入右出：暂时无法在飞书文档外展示此内容方案2：从上往下时右入右出，从下往上时左入左出：暂时无法在飞书文档外展示此内容方案3：出入共用一条边（不避让）：暂时无法在飞书文档外展示此内容方案4：出入共用一条边（避让）：暂时无法在飞书文档外展示此内容

折线实现

实现方式：

绘制方式：折线
出入方向：左入右出；若有反向调用，出入共用一条边
避让规则：跨列绘制时不避让同层节点
控制点：起点、终点、一个或两个中间点

import { Position, Rect } from '../types';

export interface Options {
  /** 起始点坐标 */
  start: Position & Rect;
  /** 终止点坐标 */
  end: Position & Rect;
  /** 间距 */
  gap?: number;
  /** 是否绘制自调用连线，默认 false */
  selfCall?: boolean;
  /** 当前起点和终点是否已被绘制过，默认 false */
  existEdge?: boolean;
  /** markerEnd x轴偏移量 */
  offsetX?: number;
}

/**
 * 绘制折线
 * - 需要计算起点、控制点1、控制点2、终点
 */
export const drawLine = (options: Options): string | null => {
  const { start: p1, end: p2, gap = 80, offsetX = 0, selfCall = false } = options;
  // 自调用取消绘制
  if (!selfCall && p1.x === p2.x && p1.y === p2.y) {
    return null;
  }
  // 间距和偏移量
  const dx = gap / 2 + offsetX;
  // 起点
  const start = {
    x: p1.x <= p2.x ? p1.x + p1.width : p1.x, // 起点在前|同列
    y: p1.y + p1.height / 2,
  };
  // 终点
  const end = {
    x: p1.x >= p2.x ? p2.x + p2.width : p2.x, // 终点在前|同列
    y: p2.y + p2.height / 2,
  };
  if (p1.x === p2.x && p1.y === p2.y) {
    // 自调用
    start.y = p1.y + p1.height / 4;
    end.y = p2.y + (p2.height * 3) / 4;
  }
  const middle1 = {
    x: p1.x <= p2.x ? start.x + dx : end.x + dx,
    y: start.y,
  };
  const middle2 = {
    x: middle1.x,
    y: end.y,
  };
  if (p1.x !== p2.x && p1.y === p2.y) {
    // 不同列同一行
    return `M ${start.x},${start.y} ${end.x},${end.y}`;
  }
  // 自调用|同一列|不同列不同行
  return `M ${start.x},${start.y} ${middle1.x},${middle1.y} ${middle2.x},${middle2.y} ${end.x},${end.y}`;
};

三次贝塞尔曲线绘制实现

实现方式：

绘制方式：三次贝塞尔曲线
出入方向：左入右出；若有反向调用，出入共用一条边
避让规则：跨列绘制时不避让同层节点
控制点：起点、起点控制点、终点、终点控制点

import { Position, Rect } from '../types';

export interface Options {
  /** 起始点坐标 */
  start: Position & Rect;
  /** 终止点坐标 */
  end: Position & Rect;
  /** 间距 */
  gap?: number;
  /** 是否绘制自调用连线，默认 false */
  selfCall?: boolean;
  /** 当前起点和终点是否已被绘制过，默认 false */
  existEdge?: boolean;
  /** markerEnd x轴偏移量 */
  offsetX?: number;
}

/**
 * 绘制三次贝塞尔曲线
 *  需要计算起点、起点控制点、终点、终点控制点
 */
export const drawCurve = (options: Options): string | null => {
  const { start, end, gap = 0, selfCall = false, existEdge = false } = options;
  // 自调用取消绘制
  if (!selfCall && start.x === end.x && start.y === end.y) {
    return null;
  }
  // 起点
  const x1 = start.x <= end.x ? start.x + start.width : start.x;
  const y1 = start.y + start.height / 2;
  // 终点
  const x2 = start.x >= end.x ? end.x + end.width : end.x;
  const y2 = end.y + end.height / 2;
  // 起点控制点、终点控制点
  let [xcs, ycs, xce, yce]: number[] = [x1, y1, x2, y2];
  if (start.x < end.x) {
    // 起点在前，终点在后
    const dx = Math.abs(x2 - x1) / 2;
    if (existEdge) {
      if (y1 < y2) {
        // 起点在上
        ycs = y1 + dx;
      } else if (y1 === y2) {
        const dx1 = Math.abs(x1 - x2) / 3;
        // 从上方圆弧过去
        xcs = x1 + dx1;
        ycs = y1 - dx1;
        xce = x2 - dx1;
        yce = y2 - dx1;
      } else {
        // 起点在下
        ycs = y1 - dx;
      }
    } else {
      xcs = x1 + dx;
    }
    xce = x2 - dx;
    return `M ${x1},${y1} C ${xcs},${ycs} ${xce},${yce} ${x2},${y2}`;
  } else if (start.x > end.x) {
    // 终点在前，起点在后
    const baseDistanceX = Math.abs(x1 - x2);
    const baseDistanceY = Math.abs(y1 - y2);
    const dx = baseDistanceX / 2;
    if (existEdge) {
      if (baseDistanceY < 20 || y1 === y2) {
        // 从下方圆弧过去
        const dx1 = baseDistanceX / 3 + baseDistanceY;
        xcs = x1 - dx1;
        ycs = y1 + dx1;
        xce = x2 + dx1;
        yce = y2 + dx1;
      } else if (y1 < y2) {
        // 起点在上
        ycs = y1 + dx;
      } else {
        // 起点在下
        ycs = y1 - dx;
      }
    } else {
      xcs = x1 - dx;
    }
    xce = x2 + dx;
    return `M ${x1},${y1} C ${xcs},${ycs} ${xce},${yce} ${x2},${y2}`;
  } else if (start.x === end.x) {
    // 同一列
    const dex = gap / 2;
    if (start.y === end.y) {
      // 自调用
      xcs = x1 + dex * 2;
      xce = x2 + dex * 2;
      ycs = y1 - dex * 2;
      yce = y2 + dex * 2;
    } else {
      // 控制点计算
      const r = Math.abs(y2 - y1) / 4;
      if (existEdge) {
        xcs = x1 + dex / 2;
        xce = x2 + dex / 2;
      } else {
        xcs = x1 + dex;
        xce = x2 + dex;
      }
      if (start.y < end.y) {
        // 同列起点在上
        ycs = y1 + r;
        yce = y2 - r;
      } else {
        // 同列起点在下
        ycs = y1 - r;
        yce = y2 + r;
      }
    }
    return `M ${x1},${y1} C ${xcs},${ycs} ${xce},${yce} ${x2},${y2}`;
  }
  return null;
};

上下游展开和收起

如何判断是否支持展开和收起上下游

展开上游：节点本身是主节点、终点或者上游节点（即 node.depth <= 0），有潜在上游且上游没有被展开。
收起上游：节点本身是主节点、终点或者上游节点（即 node.depth <= 0），有潜在上游且上游已经被展开。
展开下游：节点本身是主节点或者下游节点（即 node.depth >= 0 且 node 非终点），有潜在下游且下游没有被展开。
收起下游：节点本身是主节点或者下游节点（即 node.depth >= 0 且 node 非终点），且有潜在下游且下游已经被展开。

上下游展开和收起实现方案

方案一：修改原始数据源

优点
- 不需要考虑被展开/收起节点的粒度。
- 收起时，不需要处理上游的上游或者下游的下游。
缺点
- 布局不稳定，有新的边数据加入，会导致重新分层，节点的层级可能会变动。
详细说明
- 展开上游：查找所有 target 为被展开节点 id 的边，添加到 edges，这些边的 source 添加到 nodes。
- 收起上游：查找所有 target 为被收起节点 id 的边，从 edges 中移除，这些边的 source 标记为 upstreamIds ，其中 depth < node.depth 的节点从 nodes 移除，其余节点保留。
- 展开下游：查找所有 source 为被展开节点 id 的边，添加到 edges，这些边的 target 添加到 nodes。
- 收起下游：查找所有 source 为被收起节点 id 的边，从 edges 中移除，这些边的 target 标记为 downstreamIds ，其中 depth > node.depth 的节点从 nodes 移除，其余节点保留。

方案二：修改聚合和分层后的数据

优点
- 布局稳定，加入新的边不会影响已有节点位置。
缺点
- 计算复杂，需要计算被展开/收起节点的边关系、所有上下游关系。
详细说明
- 略

本血缘拓扑图采用方案1，上下游关系计算逻辑简单。

从零实现一个数据血缘拓扑图

背景

为什么选择自研拓扑图？

如何实现数据血缘拓扑图？

如何计算布局

如何同步布局

使用什么方案绘制边

使用什么方案绘制节点

详细实现

组件设计

拓扑图节点、连线绘制层级

拓扑图数据源

拓扑图组件结构

拓扑图组件 Props

坐标系换算

分层

层级计算方案

方案一：按边的关系累加计算

方案二：按节点和主节点的最短路径计算

方案三：按节点和主节点的“最长路径”计算

分层案例

案例1：3个节点

案例2：4个节点

案例3：5个节点

代码实现

粒度聚合和展开

PSM 粒度展开

Field 粒度聚合

数据聚合实现

边的绘制

SVG 路径绘制

SVG 动画

边的绘制场景

折线实现

三次贝塞尔曲线绘制实现

上下游展开和收起

如何判断是否支持展开和收起上下游

上下游展开和收起实现方案

方案一：修改原始数据源

方案二：修改聚合和分层后的数据

实现效果